Two main ways to model the self-organization of cortical microtubules

Cortical microtubules are components of the cytoskeleton of eukaryotic cells. They perform a very important role for the shape of plant cells controlling the synthesis of cellulose by guiding the trajectory of the plant cellulose synthase [1,2]. Indeed, microtubules form a parallel pattern at the cellular scale, thus cellulose is well organized, giving to the cell its shape, its strength, and allowing its growth to be anisotropic [3].

Microtubules are helped in these roles by microtubule associated proteins (MAPs), which can have many different properties, stabilizing or not microtubules, helping them to grow or to nucleate, walking on them carrying cargos [4]. Because it allows cells and organs to have a correct shape, the process that synthesize cellulose is important: it must be adaptive and dynamic. As microtubules are dynamic polymeric structures, that continuously grow and shrink, they allow the cell to respond to its environment.

In particular, they continuously grow by an end, the plus end and, shrink by the minus end if it is not anymore bound to its nucleation site. As the growth speed is higher than the shrinkage speed, most of the time the microtubule grows. This particular property allows the polymers to move forward even if none of the monomers moves itself. This motion is called treadmilling [5,6].

As cortical microtubules are bound to the membrane [6], they evolve on a surface, and can encounter each other.

When they meet, the growing microtubule can have three different behavior. If the angle between the two microtubules is acute, the growing microtubule will zip up with the one it meets (zippering). If the angle is wide (larger than 40°), in some cases the growing microtubule crosses over the other one (crossover), or it will rapidly depolymerize (induced catastrophe) (Figure 1) [7].

The peculiar parallel organization of microtubules in cells seems to be the sole consequence of the behavior of the microtubules when they meet.

The system formed by all interacting microtubules belongs to the class of complex systems, where new system- level behaviors might emerge from the interactions be-tween the parts of the system. In this framework, the parallel pattern of microtubules would be an emerging behavior. Such emerging properties are difficult to comprehend, and two main approaches have been used to understand the self-organization of cortical microtubules.

The first one is the particle-based simulation of all microtubules: the three behaviors that we discussed are translated into rules for the dynamics of microtubules, and the emergent behaviors are investigated. The second one is the study of microtubules as a whole: the probabilities of their orientation and the probabilities that they have one of the three behaviors discussed.

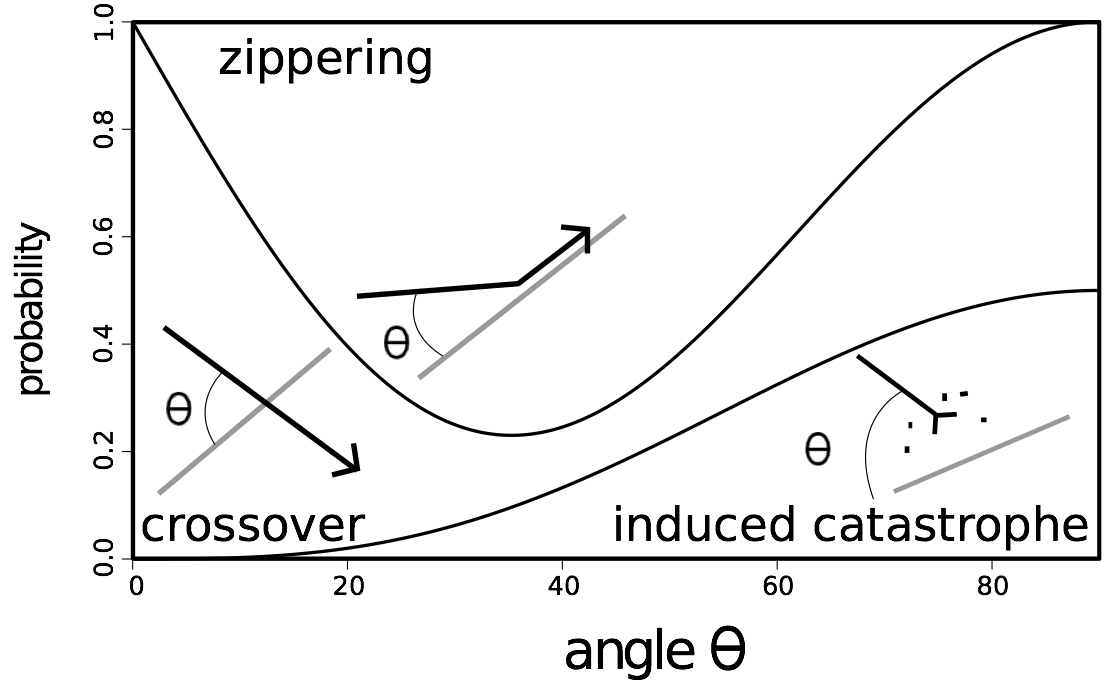
Figure 1. Schematic overview of the three processes of interaction between cortical microtubules, and their relative frequencies.

Schematic overview of the three processes of interaction between cortical microtubules, and their relative frequencies.

For instance, if the angle is 45 degrees, the probability of zippering is 0.45, that of crossover is 0.25 and that of catastrophe is 0.3.

One way to understand the behavior of cortical microtubules is to model each one of them.

One technique to observe an emergence is to compute microtubules, giving them a few rules to follow when they encounter another microtubule, between zippering, crossover and induced catastrophe. The system then evolves by itself, and leads or not to the parallel pattern observed in vivo .

The methodology followed to model cortical microtubules is always similar.

First, initial microtubules are randomly laid down. Then, for each step of time, each microtubule will grow from the plus end. Sometimes it will decrease from the minus end, but it is not done in all the simulations since the shrinkage is low most of the time.

When a microtubule encounters another one, it will react depending on the angle between the two microtubules. If the angle is acute, the growing microtubule will surely zip with the other, if the angle is wide, it will either cross over the other one, or depolymerize. In addition, some microtubules can be nucleated.

Then, another step of time happens, and the process is done once again, until the simulation ends.

Probabilities of the different events can differ between simulations. For example, Eren et al.  [8] chose that if the angle between the two microtubules was lower than 40°, the microtubule would zip. In the other case, it will crossover 70% of the time, and shrink 30% of the time, while Tindemans [9] chose the density function showed in Figure 1:

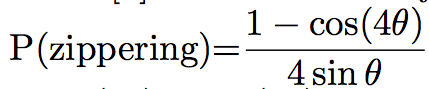
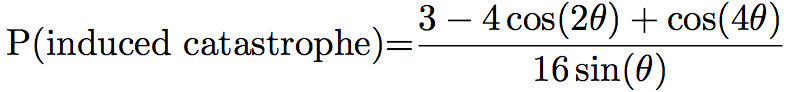
The simulation often allows the user to see the microtubules during the simulation, and the pattern of microtubules at the end of the simulation (Figure 2). They can then be studied and compared to the in vivo pattern. The organization of microtubules can be quantified by measuring the angles between microtubules (Figure 2). If all the angles are close, then microtubules are aligned. Otherwise, microtubules are not.

These simulations can help to understand what are the necessary conditions to allow the emergence of the pattern of microtubules we observe in vivo , and to understand the roles of the different actors.

This methodology is quite close to the reality, but the computation of all the trajectories and the encounters can take a long time, and much memory on computers.

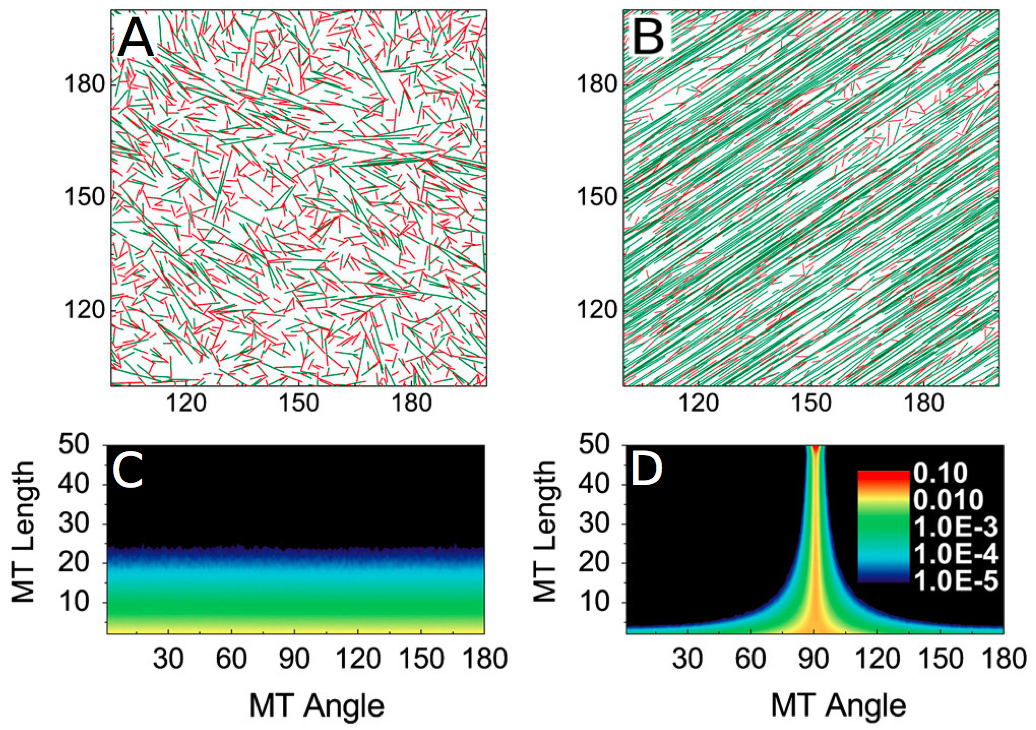
Figure 2. Example of (A) a simulation with no self-organization of microtubules, (B) a simulation where there is an emergence of an organization of the micro­tubules.

Example of (A) a simulation with no self-organization of microtubules, (B) a simulation where there is an emergence of an organization of the micro­tubules.

The way used to quantify the alignment of microtubules is the orientation of the microtubules, as shown in (C) and (D) . The more warm the color is, the more microtubules there is. When there is an alignment, the majority of the microtubules follows a predominant angle (D). (Reproduced from Shi et al. [10]).

The probability-based approach uses another way to understand the dynamics of microtubules, which does not need computation. It considers the density of growing microtubules, the probability that this density has to meet another microtubule in the same density, and the angle of the collision.

Microtubules have a probability to have one or another behavior, among zippering, crossover and induced catastrophe. This approach will actually consider that the microtubule is at a certain percentage shrinking, at another percentage in a zippering, and at a third percentage growing over the other microtubule, in a probalistic formulation, what means that these three behaviors happen at the same time.

Then, differential equations representing flux of growing, shrinking microtubules can be laid down, also taking into account their density and their orientation.

For example, Hawkins [9,11] defined several densities of straight segments of microtubules i . Each segment i is straight. When a microtubule zips, its orientation changes. The microtubule will then be the succession of two segments, the first ( i ) following the ancient orientation, the other ( i+1 ) standing for the new orientation. Plus, they distinguish the active segment, which grows ( + ) or shrink ( - ) from the inactive ( 0 ) segments. The densities of segments i of microtubules studied are mσi (l,θ,t), where σ ∈ +,−,0 is the state of the microtubules, l the length of the microtubule and θ its orientation at time t .

Each microtubule i is straight. When it undergoes a zippering, its orientation changes, so there is a creation of a new microtubule i+1 , with another orientation. The former straight segment still exists, but it is paused, and does not grow anymore. It can be reactivated if the new segment shrinks towards the former.

Thus, i gives the number of times that the microtubule has undergone a zippering.

Therefore, the total length density k(θ, t) is given by:

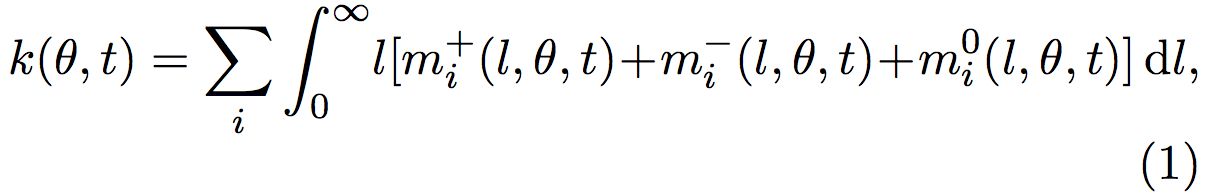
where k(θ,t) is the sum over all the i microtubules, of all the l possible lengths.

The density and the orientation of the microtubules fluctuate when time goes on, depending on the rates of zippering, crossovers and catastrophes. Indeed, when a growing microtubule (m_i ⁺ ) undergo an induced- catastrophe, it becomes a shrinking microtubule (m_i ⁻ ). Changes in the microtubule behaviors cause changes in the numbers of growing (m_i ⁺ ), shrinking (m_i ⁻ ), and inactive segments (m_i ⁰ ). These changes can be quantified by the following equations, where each Φ represents a behavior:

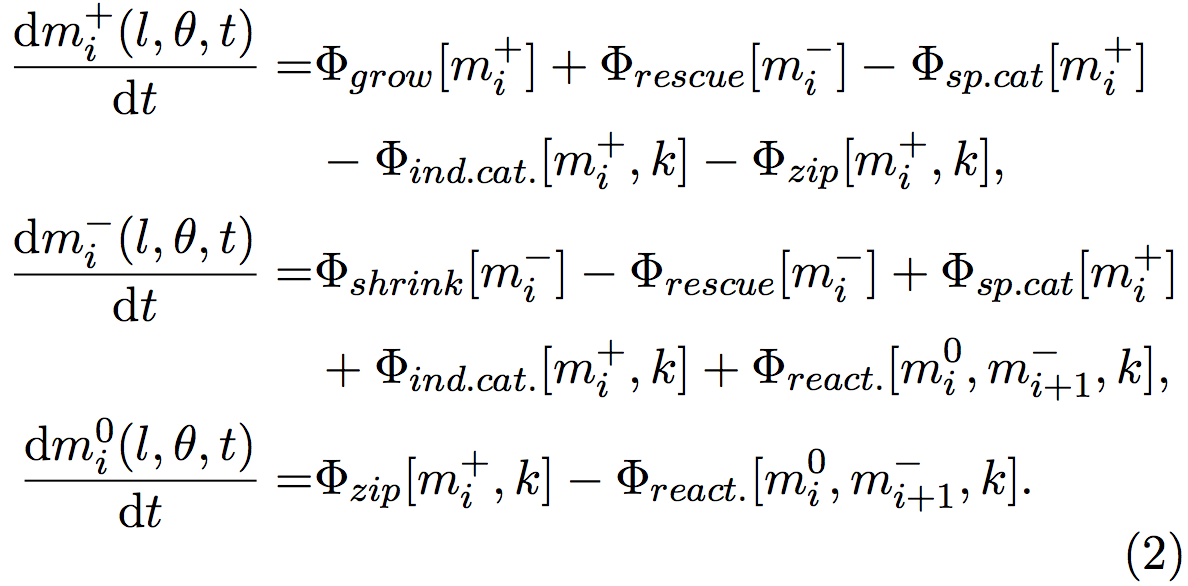
Φ grow and Φ shrink represents microtubules that respectively grow and shrink. Φ rescue stands for microtubules that were shrinking and that start to grow, Φ sp.cat and Φ ind.cat. microtubules that were growing and begin to shrink because of spontaneous or induced catastrophes. Φ react. symbolizes microtubules that were reactivated from an inactive state and start to grow.

Φ zip is a particular case, since when a microtubule zips, its orientation changes and a new segment is created. The old segment is inactivated (become a m_i ⁰ when it was a m_i ⁺ ) and a new segment starts to grow. The nucleation of this new segment is handled by other equations not shown here.

For example, the events that lead to the increase of the group m_i ⁺ (l,θ,t) consist in the microtubules that grow and so their lengths change Φ grow [m_i ⁺ ], the microtubules that were shrinking m_i ⁻ and that has been rescued (Φ rescue [m_i ⁻ ]). The events that lead to a decrease are the microtubules that were growing and that spontaneously shrink (Φ sp.cat [m_i ⁺ ]), the microtubules that were growing, and that start to shrink because they encountered another microtubule (Φ ind.cat [m_i ⁺ ]), and finally the segments of microtubules that were growing, and that stopped because of a zippering, another segment been nucleated with a new orientation (Φ zip [m_i ⁺ ]).

The new segment is also growing, but as its length is null, this is handled by another equation.

Φ values can be calculated from biological quantitative studies [3,6,12], for example here, Φ sp.cat [m_i ⁺ ] = r_c m⁺ , where r_c is the rate of spontaneous catastrophe, measured by biologists.

Crossovers do not influence the growth of microtubules, so the analogous term for this event is not used here. The system evolves into a stable state when the m_i ⁺ , m_i ⁻ and m_i ⁰ quantities become stable, and do not change over the time. Then the properties of the organization of microtubules can be studied, such as the final density of microtubule, or the anisotropy of the system, i.e. the alignment of the microtubules (Figure 3).

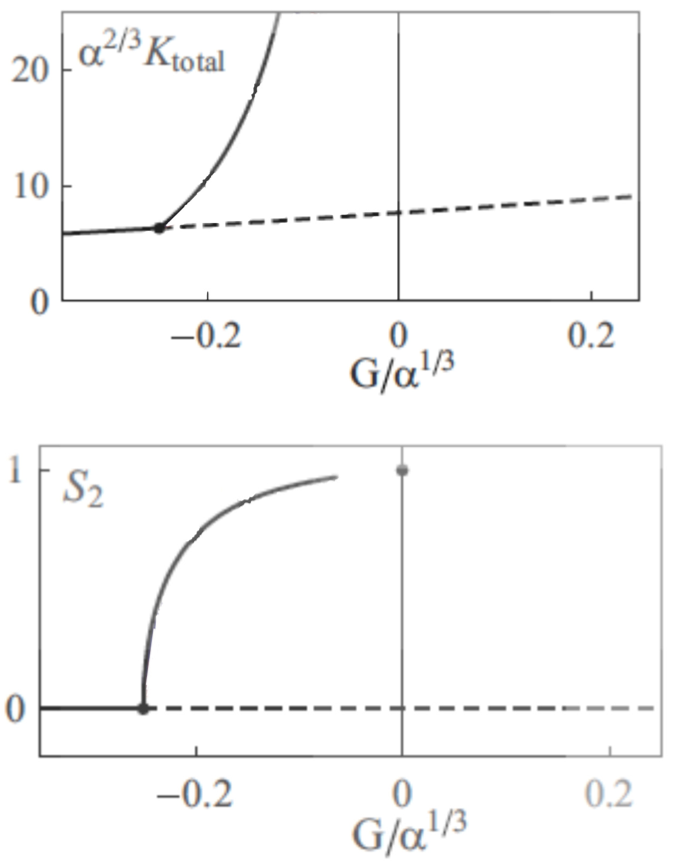
Figure 3. Bifurcation diagrams representing the stable organization of microtubules.

Bifurcation diagrams representing the stable organization of microtubules.

α is the probability of crossover when the angle between the two microtubules is 90°, G is a parameter that depends on the growing, shrinking velocities, and the rescue, spontaneous catastrophe and nucleation rate. When G increases, microtubules are more stable. K_total is the density of all the microtubules, and S2 is the so-called 2D nematic order parameter: when S2 is zero, the organization of microtubules is anisotropic, whereas when S2=1, all the microtubules are aligned. (Reproduced from Hawkins et al. 2010 [11]).

These models gave several results on the dynamics of cortical microtubules, but the two approaches are very different, and the correlation between the results are not necessarily clear.

In a probability-based study, Hawkins et al.  [11] showed that the pattern observed at the cellular scale was mainly due to the catastrophes, which deleted the wrong oriented microtubules.

Hawkins showed that if microtubules overcame only zippering and crossovers, they did not self-organize. The zippering alone was not sufficient for the emergence of the pattern.

On the contrary, particle-based simulations showed that the bundling of microtubules by zippering was the most important factor. In those studies, induced catastrophes had not such an importance [13,8]. However, they conceded that induced catastrophes helped the system to get its organization faster, and that the balance between the different parameters was very important [4,8].

Other researchers considered both approaches and studied whether they are similar or not. For example, Shi et al.  [10] studied both the particle-based approach and the physical approach, changing densities of microtubules and plus-end polymerization rate.

The results of these simulations can be gathered in phase diagrams (Figure 4). These two diagrams seem close, so the phenomena that are studied are qualitatively close. But as the scales and the values are quite different, the quantitative values that are extract from these studies can not easily be compared.

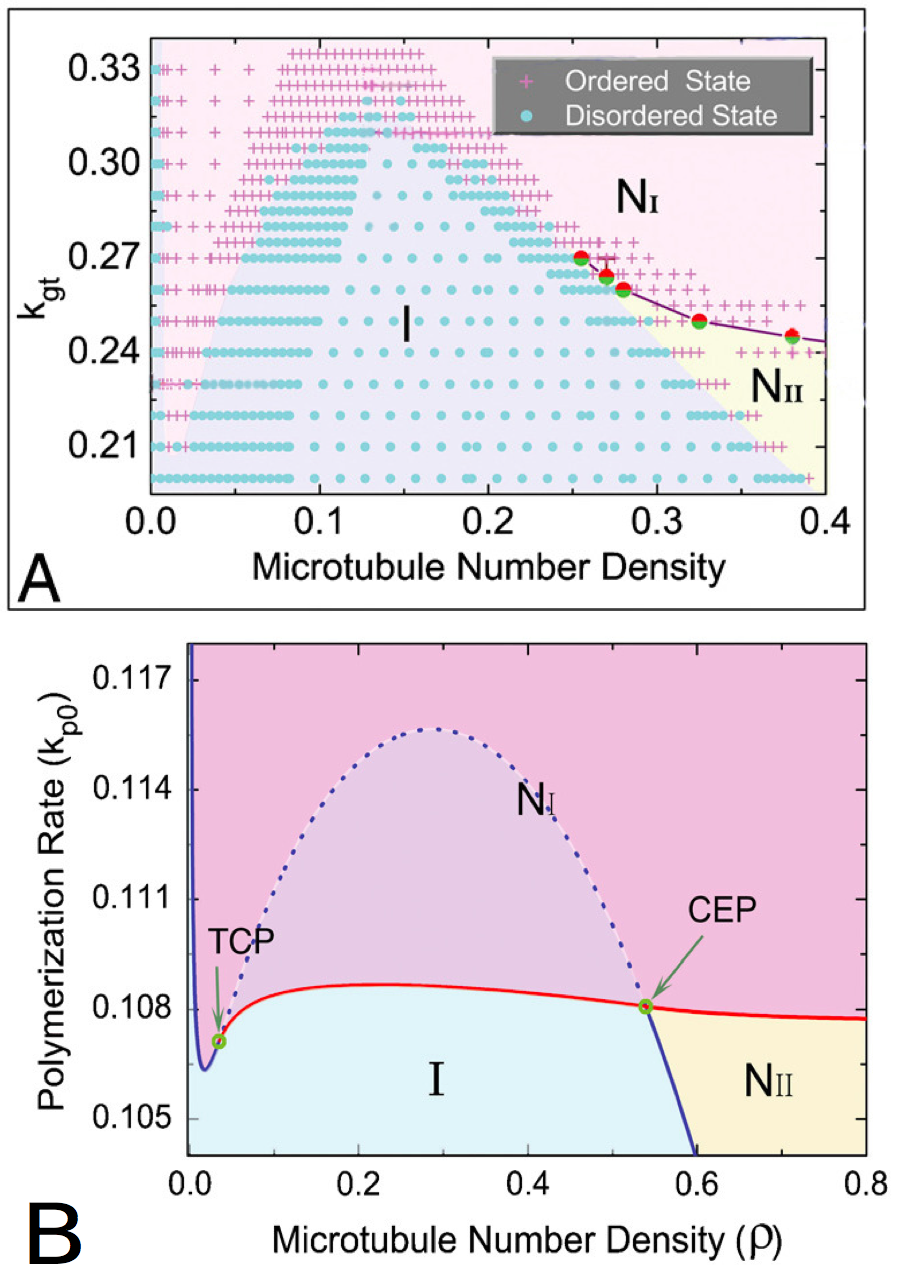
Figure 4. Phase diagrams given by the particle-based approach (A) and the probabilistic approach (B),

Phase diagrams given by the particle-based approach (A) and the probabilistic approach (B),

with the isotropic phase (I), nematic I phase (NI), and nematic II phase (NII ). The points in A represents distinct simulations ran with different parameters. The tricritical point (TCP) and the critical endpoint (CEP) (B) are theoretically perfectly determined. The patterns are qualitatively close, so the conclusions made by the two approaches are similar, but the quantitative values are quite different. Besides, the second studied parameter is not exactly the same in both the graphics, even if it represents the same quantity : in (A), k_gt is the growth rate of the plus end of the microtubules, in (B), k_p0 is the polymerization rate of the microtubules. (Reproduced from Shi et al. [10]).

The two methodologies differ concerning other aspects, because of the approaches themselves.

In particle-based approaches, when a growing microtubule encounters a bundle, it meets one after the other all the microtubules of the bundle. In probability-based studies, mean densities of microtubules are studied, so no bundles can be observed. In these studies, each microtubule is considered isolated.

If particle-based simulations disregard zippering, which accounts for bundles formation, results of the two approaches are close (Figure 5.a). If bundles are formed during simulations (Figure 5.b), results are different. When bundles are considered as a sole microtubule (single collision), results are closer.

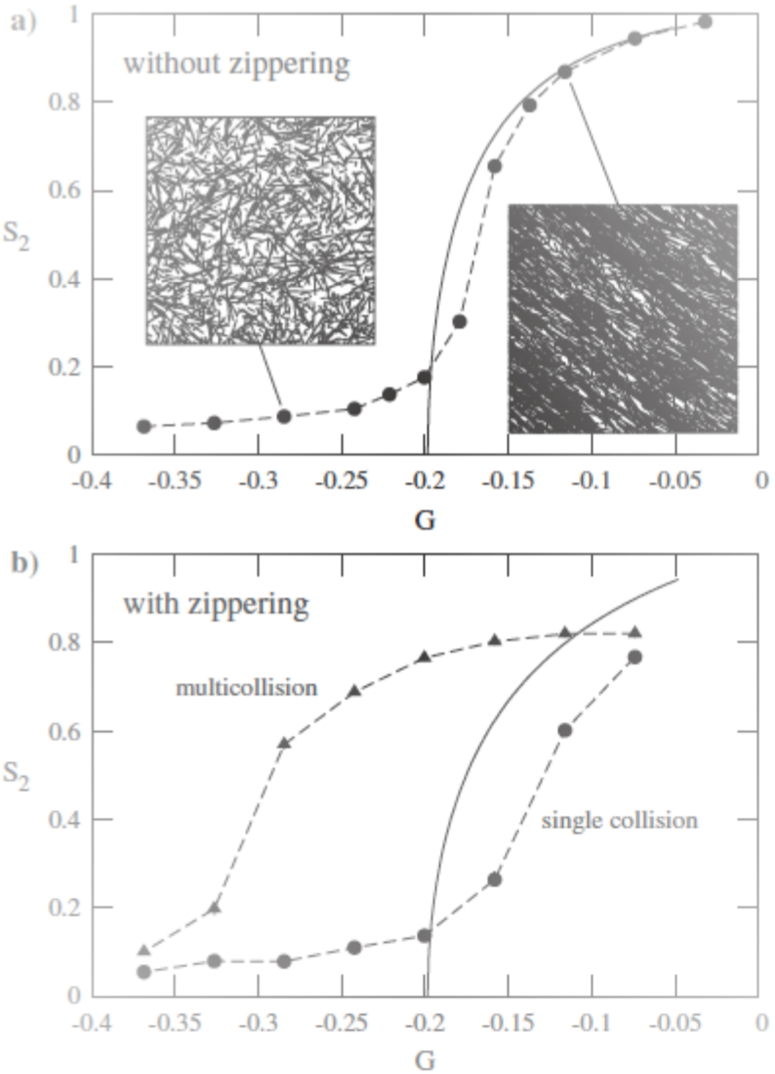
Figure 5. Comparison between theoretical (solid lines) and simulation results (symbols).

Comparison between theoretical (solid lines) and simulation results (symbols).

G is a parameter that depends on the growing, shrinking velocities, and the rescue, spontaneous catastrophe and nucleation rate. When G grows, microtubules are more stable. S2 is the so-called 2D nematic order parameter. The handling of bundles causes different results between the pariticle-based and probability-based simulations. (Reproduced from Tindemans et al. [9]).

The handling of bundles is one of the main differences between the two approaches. It could explain why physical studies showed that the organization was mainly due to induced catastrophes [11], whereas particle-based studies showed on the contrary that zippering had a prominent role [8,13].

Microtubules are growing polymers. As every protein in cells, they are associated to other proteins, called MAPs (microtubule associated proteins). Many different MAPs exist, which can have diverse functions [14,15]. Specific MAPs are associated to cortical microtubules, such as MOR1, FRA2, CLASP [12,16‑18]. The function of these proteins can frequently be mapped to model parameters. MOR1 can alter several dynamic instability parameters, such as growing and shrinkage velocities. Changing these parameters in the model can some time be enough to cause the emergence of the same pattern as in vivo .

Velocities have been measured on this mutant. Parameters of particle-based simulations have been modified depending on the quantitative values measured on mutants [13]. Changing velocities in the model showed same patterns of self-organization of microtubules as in the mutant.

Another important MAP is FRA2. It is a katanin-like microtubule-severing protein: this MAP cuts microtubules, making them more dynamic. Fra2 mutants show less organized cortical microtubules [19], because if FRA2 is not active, microtubules are locked to their nucleation site, and cannot be reorganized depending on other microtubules they meet [20]. This mutant has been tested [8], with velocities and quantitative values measured on mutants. A disorganization was observed, close to what was observe in mutants.

Another studied protein is CLASP [18]. It seems that this protein allows microtubules to curve and have an angular trajectory, what they should not since their persistence length is very high.

This protein is localized at the edges of the walls of cells, and allows cortical microtubules to go around corners of the membrane of the cell.

Without CLASP, angles between the two walls are wide, so all microtubules would undergo an induced catastrophe. CLASP allows microtubules to curve, thus they can go from one side to another.

Ambrose [18] used a particle-based simulation to study the influence of CLASP, and showed that its localization on the edges of cells can be important for the organization of cortical microtubules, since it allows or not microtubules to link up two sides of the cell.

If the upper and the lower side do not have CLASP on their edges, microtubules will have a specific organization, where they will run around the cell without going on the upper and the lower sides. The cell would therefore have an anisotropic growth, as seen in real cells. Thus, a change in the distribution of CLASP could change the direction of growing of the cell, and the shape of the organ.

Gravity has an impact on the dynamics of cortical microtubules and their in vitro self-organization [21,22]. Indeed, growth of cells is disrupted when cells grow in low gravity [23], and that the expression of some genes is modified [23]. These conditions also impact microtubules: when they grow in low gravity conditions, they show almost no self-organization and are disordered [22]. They have an isotropic configuration.

Some modeling experiment has been done to understand the impact of gravity on the self-organization of microtubules [22,24]. Taking in account the gravitational drift of microtubules, microtubules can self-organize in striae. Microtubules co-aligned and formed structures at an upper scale.

Other aspects than genetics and MAPs affect the organization of microtubules.

For example, electrical or mechanical fields that do not cause wounds reorient microtubules for a period of 6 hours, in a direction perpendicular to the applied field [25,26].

Microtubules fill an important role responding to mechanical stresses, because they are ubiquitous in plant development [27]. Correct development of plants would require the mechanical sensitivity of microtubules, for cells and organs to have the right shape.

The importance of mechanical stress has been studied in shoot apical mersitems, where organs start to grow and where the primary shape of the organ is formed [28]. Different MAPs and actors are candidates to link mechanical stress and microtubule organization [29,30], such as AtMSL9 and AtMSL10 [31], which are mechanosensitive channels in Arabidopsis thaliana , which respond to tension in the membrane.

Mechanical stresses are very important for the correct development of plants, but mechanisms are not well understood and no model has been developed to explain this behavior.

Besides, cortical microtubules seem to be implied in several stress responses, such as salt stress, drought, and low temperature [32]. Indeed, these stresses would have an impact on several MAPs, which would then have an impact on microtubules and their organization. It was known that cells had response mechanisms, but it seems that cortical microtubules are by themselves sensors of these stimuli.

The way they fill these roles remains unclear, and show again how important microtubules are for the cell. Including these aspects in models could be interesting to study the link between dynamics of microtubules and their role as sensors.

Dynamic of cortical microtubules has been modeled, to understand the underlying phenomena leading to the parallel organization observed in vivo . To assert the validity of these models, some mutants of MAPs have been studied, such as mor1 , fra2 or clasp , showing results similar to what was seen in in vivo experiments [8,13]. Mechanics has an important role for the self-organization of microtubules [28], but the link between mechanical stress and self-organization of microtubules has not been much studied by modeling. The modeling of the influence of mechanical stress could allow scientists to better understand what are actors linking mechanical sensors and microtubules, and their organization.